面積の基本①(x軸方向への定積分) 面積の基本②(y軸方向への定積分) 接線と面積, 接する2曲線と面積;About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators皆さんは、円の面積が $$$ S = \pi r^2 $$$ となることを知っていると思います。小学校か中学校で習ったでしょう。 では、なぜ円の面積が $$$ S = \pi r^2 $$$ となるかわかるでしょうか。 実はこの公式は積分計算で導くことができるんです。

円の部分面積と部分円周を教えてください 添付にある円のcの面積と 数学 教えて Goo
円 面積 積分 極座標
円 面積 積分 極座標-円の面積について 将来、三角関数の積分を利用して円の面積を簡単に計算することになるが、ここではもっと原始 的に円を取り扱ってみることにする。 1 πについて どの円も全て相似であることにまず注意する。なぜなら、二つの円を円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積 弓形の面積(中心角から) 弓形の面積(弓形の半径と高さから) 弓形の面積(弓形の弦長と高さ
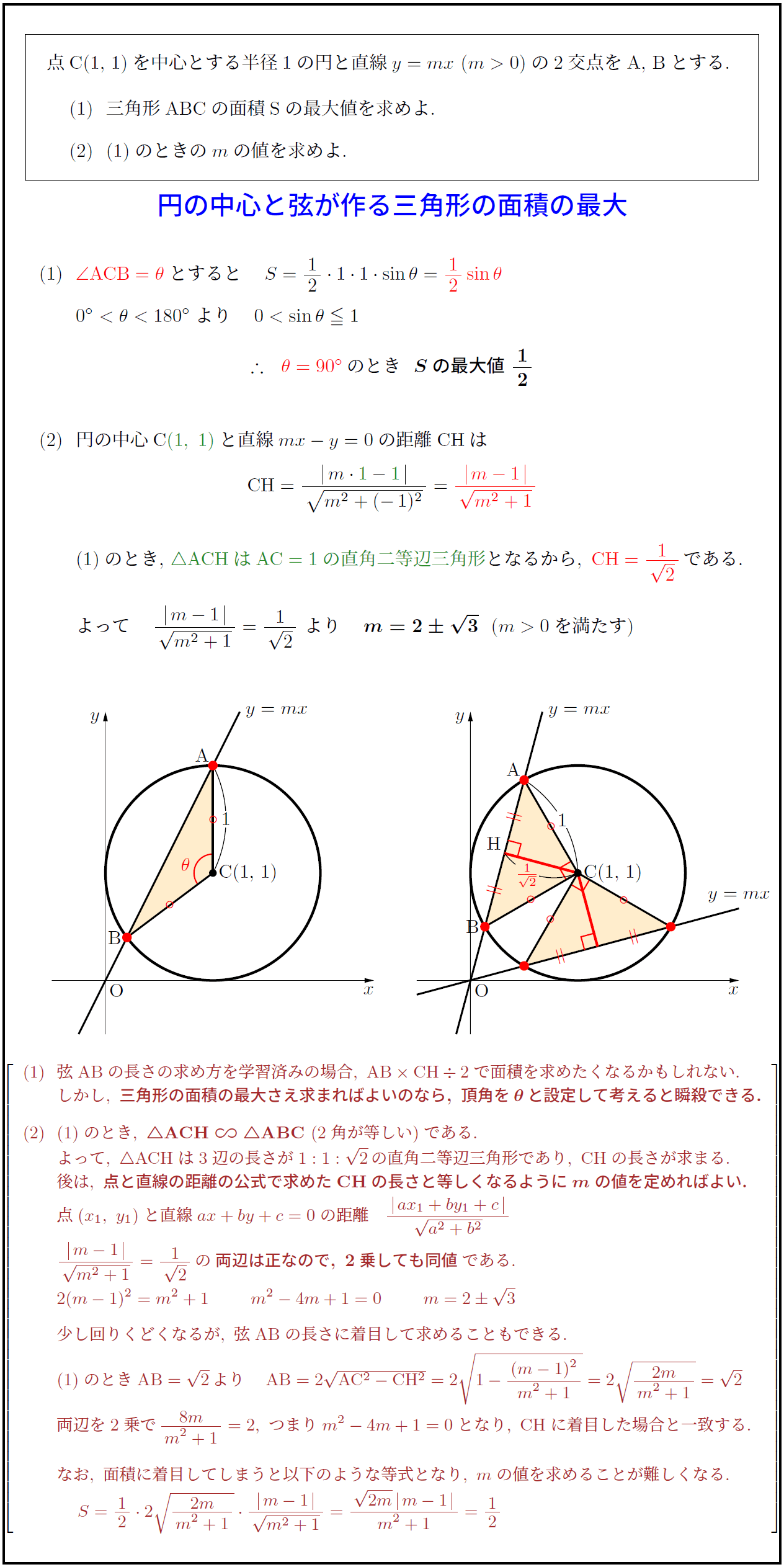



高校数学 円の中心と弦が作る三角形の面積の最大 受験の月
面積, 微積分, 円, 二次曲線, 定積分, 不定積分, 極限, 放物線 Archimedes(BC287? ~BC212) 前期アレクサンドリア学派の中で、アルキメデスは特別な存在。半径 の薄い円盤がある. を面密度(単位面積あたり の質量)とする.ただし は円盤の中心からの距離とする. Ex311 R r = (r) (r) = 0 1 r2 R2 ⇥ であるときこの円盤の総質量 を求めよ.M 面積分の応用 Ex312 半径 の球の体積 を面積分を使って求めてみよ.R V円の面積をめぐる循環論法からの脱却のために 半径a の円の面積をS と書く。 このとき S = ˇa2 =) lim h!0 sinh h = 1 =) (sinx)′ = cosx ∫ a 0 √ a2 x2 dx = ˇa2 4 =) S = ˇa2 が成り立つことはさまざまな書物で示されているが、これは循環論法である
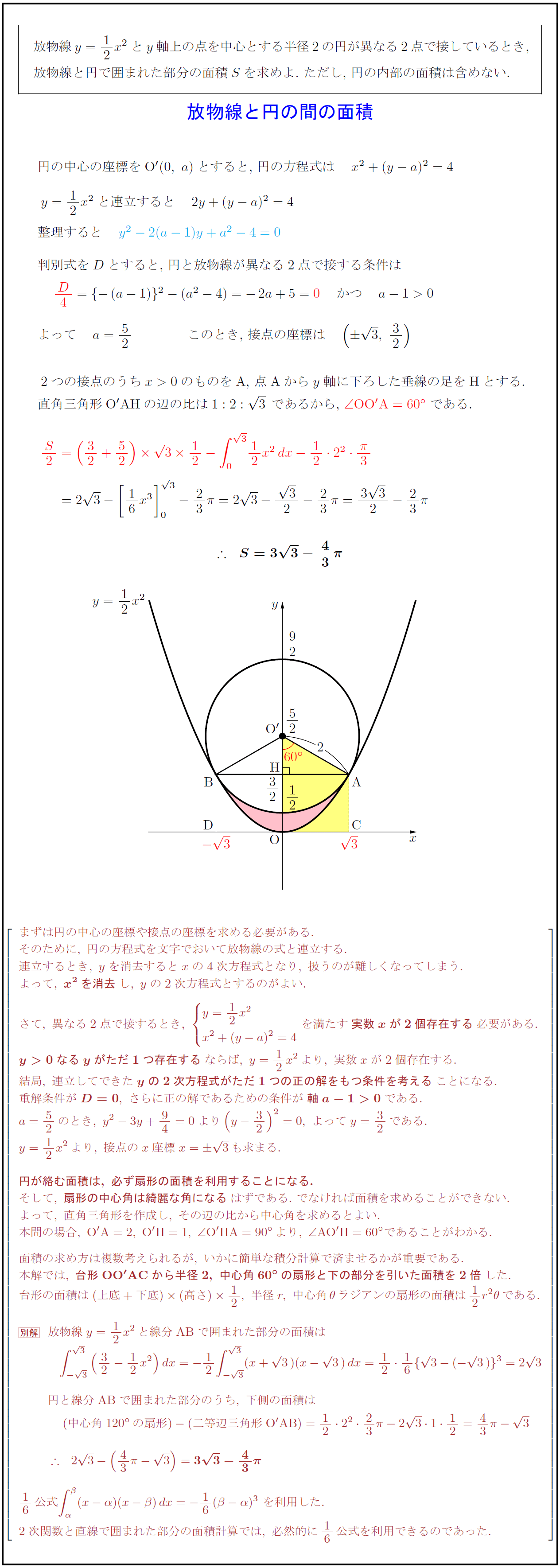
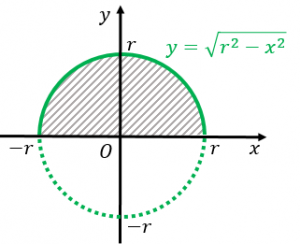
円AとCに囲まれた図形は、図Bの青い部分と黄色い部分の2つ。 そのうち、 x 軸よりも上にあるもの、つまり青い部分の面積を問われている。 図Bの青い部分は y 軸に関して対称なので、 y 軸より右の部分の面積を求めて、2倍する方針で解く。 ところが、数 円の面積を求める方法の1つに、2次元極座標で 方向と 方向の格子に分割して、 を計算する方法がありますよね。 この場合、積分する微小領域の形を縦と横が と の長方形とみなして、その積 をその面積としていると見なせます。 しかし微小領域は厳密に表面積は半径の二乗に比例し,体積は半径の三乗に比例することは感覚的に明らかです。 よって,公式を覚えていなくても S = A r 2 , V = B r 3 S=Ar^2,\V=Br^3 S = A r 2 , V = B r 3 ということが分
曲線x a +y b =1の面積とベータ関数B(p,q) 交点が求まらない面積による2等分(等積条件)x sinxdx;(沖山, 06, pp), 半径1の円の面積がπで あることを活かして円の面積公式を導出する授業(萬, 06,pp8593)およびそれぞれの授業に関する考察 がある。 しかし,高校数学の授業で極限の概念を獲得し,微 積分を学習した後に,改めて様々な積分領域が変数に依存する場合の重積分 積分順序の変更 変数変換:ヤコビ行列式 == 閉曲線で囲まれた図形の面積 == 基本 右図のような図形の面積は, S= b∫ awww{ f (x)−g (x) } dx で求められます. 例1 円 x 2 y 2 =4 の面積 円 x 2 y 2 =4 の方程式を y




くろべえ 卵焼きの失敗と 2円の重なり部分の面積




扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ
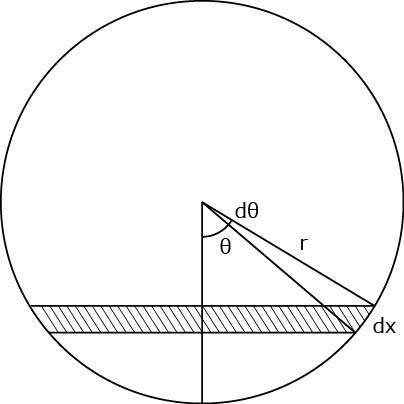
平行四辺形の面積(底辺と高さから) 平行四辺形の面積(2辺と夾角から) 円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積 弓形の面積(中心角から) 表面積を積分する(足し合わせる)と体積になる。 つまり、体積の微分が表面積。 \((\displaystyle\frac{4}{3}\pi r^3)'=4\pi r^2\) おまけ 円錐を積分で計算してみましょう。 底面の半径\(r\)、高さ\(h\)とする。 底面の中心を原点に、頂点に向かって軸を取る。積分式: s=4∫(1-x 2 ) 1/2 dx (4分の1円の面積x4) ここで、積分の範囲は0から1までです。 極座標の変換式とそれを用いた円の面積の積分式は、 変換式: x=cosθ y=sinθ 積分式: s=4∫(1-cos 2 θ) 1/2 (-sinθdθ)



Object 01



基礎からわかる電験3種の数学図形 基礎からわかる電気技術者の知識と資格
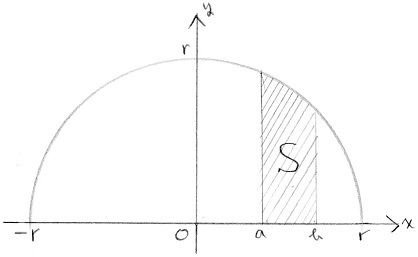
断面積、積分区間を調べたら、あとは体積の積分公式に当てはめるだけです。 解答 半円を \(y = \sqrt{a^2 − x^2}\) とおき、\(\mathrm{Q}(x, 0)\) とする。やり方としては、まず求める面積を とし、それを右図のように2つに分割してそれぞれを と置きます。 の間では さらに の間では といった感じで積分領域を区分けし、これを計算していきます。 さらに、それぞれの円の扇形から三角形を引いたものを足せば赤色の面積が求められることが見えます。 図のように角度θ1、θ2を置くと、 s = ((円o1の角度θ1扇形の面積) (円o2の角度θ2扇形の面積) (三角形ao1o2の面積)) * 2 と求められます。



円の面積の求め方を教えてください 4分の1の大きさの円 です Yahoo 知恵袋




円の面積の求め方 公式と計算例
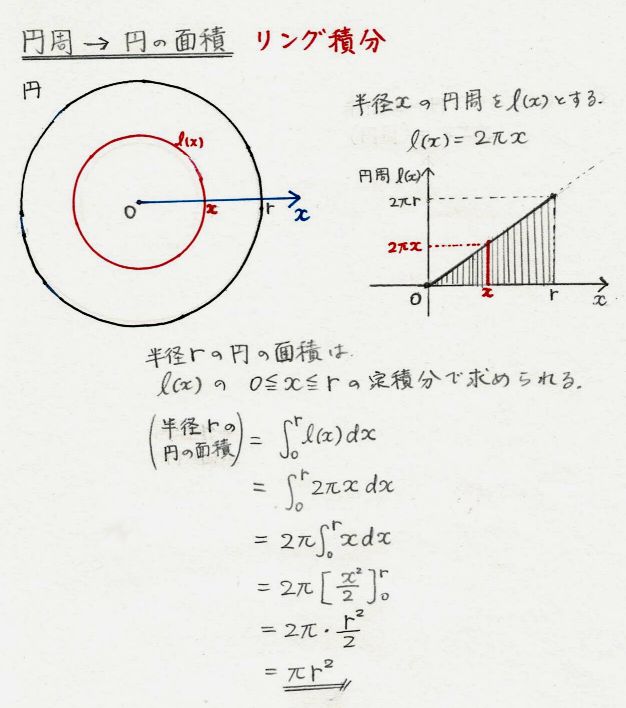
積分で言えば、円の半径rを少しずつ増やしながら、 表面積を足していくと体積になるのです。 NO117 6/5 ヴァー 円に関する微分(6)例 3 15 (, 両方に単純な領域における多重積分) 領域 を下図のような三角形の領域とする.このとき多重積分 を求める. 被積分関数は であるから, 領域 の面積を とすると, となる. 領域下のような微分と積分の関係が成り立ちます! くだけた表現をすると、 円周を積分 = 円の面積 球の表面積を積分 = 球の体積 逆に、 円の面積を微分 = 円周 球の体積を微分 = 球の表面積



ベクトルポテンシャル補足 12 での 球の表面積 を求める証明 Jo3krpの独り言



問題93おうぎ形の面積
なので、 $0$ から $3$ まで積分するということは、この円の右上の部分である $\dfrac{1}{4}$ を表しているので、\ \frac{3^2}{4}\pi \となり、これを $\dfrac{8}{3}$ 倍して、楕円の面積が $6\pi$ とあることがわかります。面積分 ベクトル解析 における 面積分 (めんせきぶん、 surface integral )は、 曲面 上でとった 定積分 であり、 二重積分 として捉えることもできる。 線積分 は一次元の類似物にあたる。 曲面が与えられたとき、その上の スカラー場 や ベクトル場 を これは半径3の円の上半分を表す方程式であるから,\ 本問の図形的意味は右上図の面積である どちらの解法が有利かは火を見るより明らかである {∫{a²x²}dx\ 型の定積分は,\ 必ず円の面積の一部とみて求めよう \求める定積分は,\ 右図の面積に等しい




円の面積の求め方 公式と計算例




円の面積 Java実験室
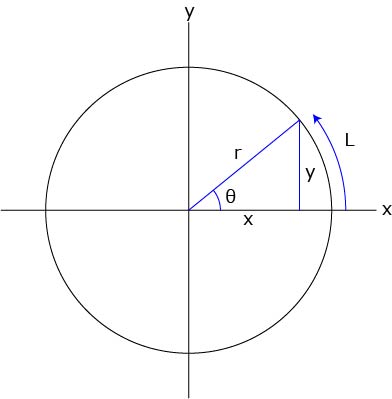
すると円の面積 S S は S = πR2 S = π R 2その積分を身体で感じるために、簡単に求まる円の面積を積分で求めてみよう。 円の面積の積分を式で表してみると、 ∫√(r 2 -χ 2 )dx である。 よって面の範囲を考慮すると積分範囲は θ : 0 → π, ϕ : 0 → 2π となるため、面 S2 上での面積分は ( 11 )と ( 12 )より ∬S2→ ⋅ d→S2 = ∬S2(4sinθcosϕ, 4sinθsinϕ, 4cosθ) ⋅ (sinθcosϕ, sinθsinϕ, cosθ)4sinθdθdϕ = 16∫π 0dθ∫2π 0 dϕ(sin2θcos2ϕ sin2θsin2ϕ cos2θ)sinθ = 16(∫π 0sinθdθ)(∫2π 0 dϕ) = 16 − cosθπ0 ⋅ 2π = 16 ⋅ 2 ⋅ 2π = 64π となる。




数学の伝道師 秋山仁さん 算数を勉強しないと損 子どもを算数好きに育てるには 親子で挑む 算数つまずき攻略法 朝日新聞edua
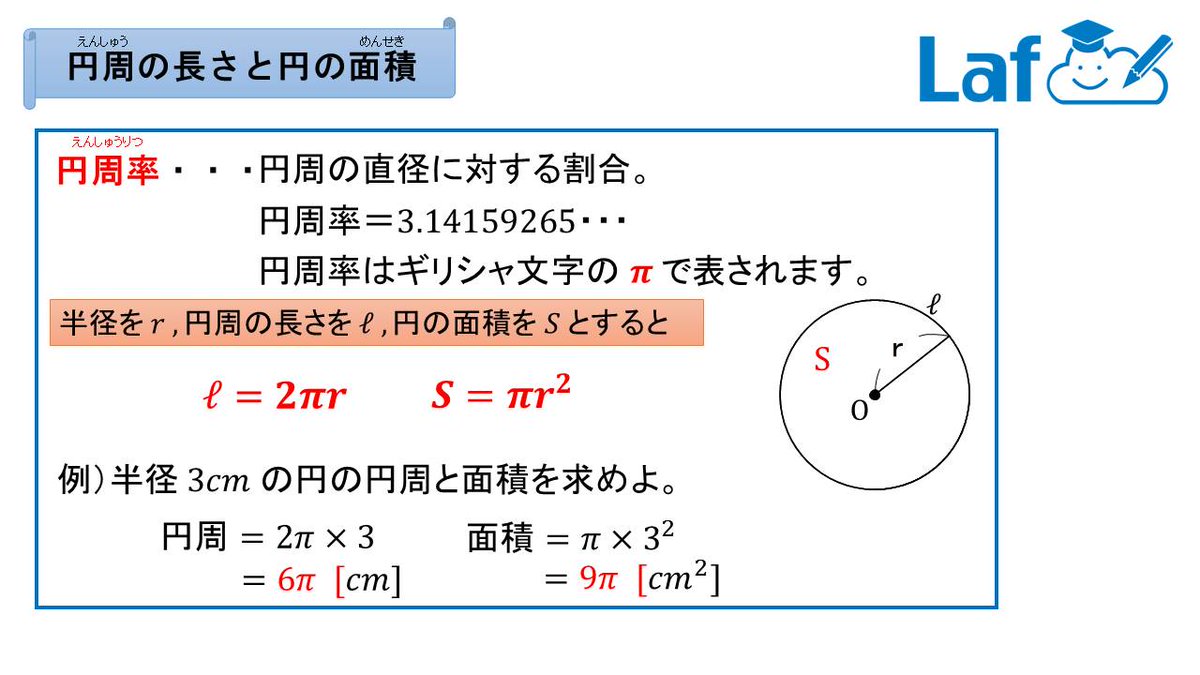



円の面積 直径
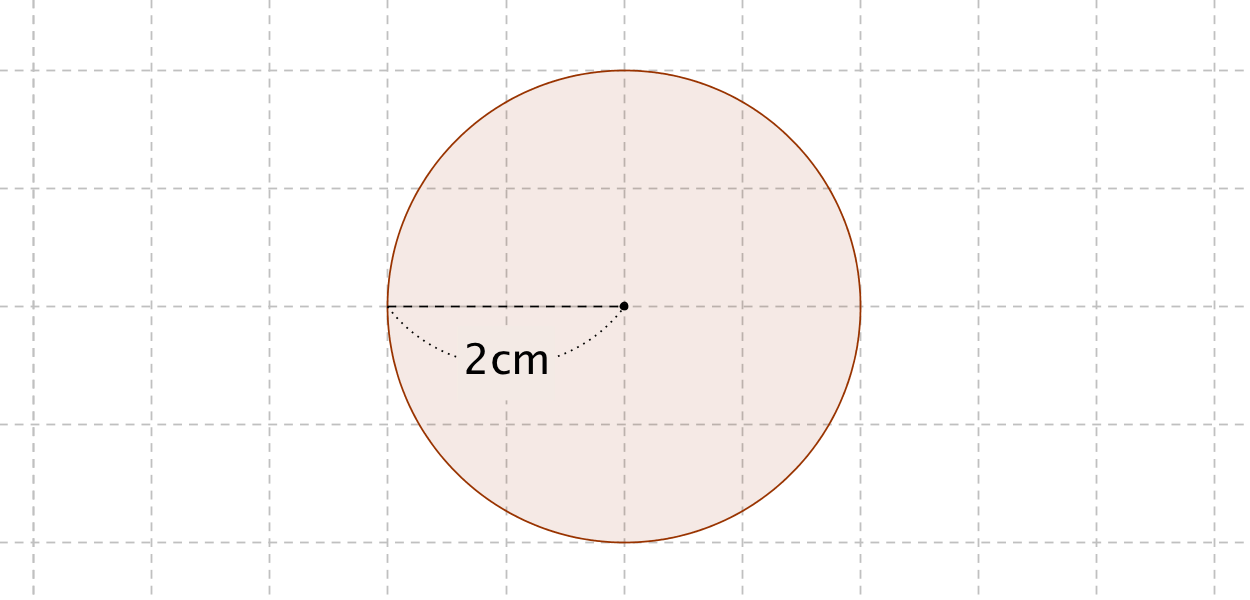
日常を数式を通して見るシリーズ。今回は円と楕円を行ったり来たりしながら、楕円の面積に関する性質を見ていく。シリーズの前回は 観覧車のゴンドラをぐわんぐわん揺らしたい ヨーキョクデイ ということにしておく。 円と楕円と線型変換 まず、 として、次の方程式で表される楕 円の面積 半径 半径 円周率 円 の 面 積 = 半 径 × 半 径 × 円 周 率 = 4 × 4 × 314 = 5024 c m 2 と求まります。 問②面積が c m 2 の円の円周の長さを求めてください。 (円周率は 314 ) 円の面積の公式から半径を計算したあと 「半径⇒直径⇒円周の長さ」の順に求めていきます。 公式に当てはめることで、円周の長さが 4396 c m と求まりました。 求める面積は、上図の青色で塗られた部分になります。 理論計算上は、円の面積は、πr 2 で求まるので 1/4円の面積は、m 2です。 これを、数値積分で求めてみます。 台形面積
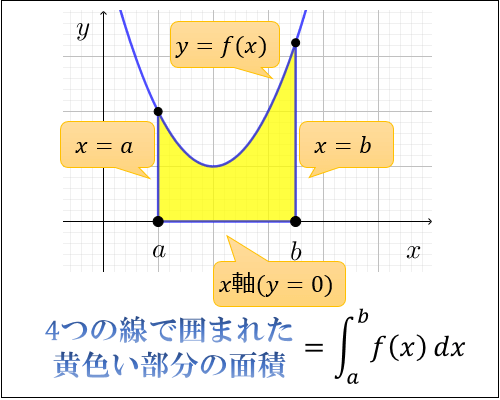



積分とは何なのか 面積と積分計算の意味 アタリマエ



数学 球の表面積を積分で計算してもうまくいかない人へ
左図において、1辺が a の正方形の面積は、 である。 逐次積分の計算例1 円の内部及び周 x 2 +y 2 二重積分 を計算せよ。 (解) (終) 値が 0 になることは、グラフからも推察される。 逐次積分の計算例2 二重積分 を計算せよ。式で定義していた。縦線形d の面積という概念は、小学校で円の面積につ いて習いわかったつもりになったものとして取り扱っている。高校で習った ように面積や体積を求める計算として積分を用いる分には、このような設定 でも大きな破綻は生じない。微小面積は、単位幅当りの値です。 これを、「b」という長さに渡って合計すれば、長さa×bの面積が算定できます。 微小面積をbという長さ分、積分すれば、 a×(11・・・・=b)=a×b です。 ※(11・・・・=b)とは、単位幅をbになるまで加えることを意味します。 上記より、積分で四角形の面積を計算しました。 「微小面積を合計する」ことが、積分の



円の面積を 一般的に知られている公式を使わずに算出する方法を教えてくれませんか Quora




媒介変数表示された曲線のグラフの面積 基本編 おいしい数学
円の面積を正確に表すには、記号 π {\displaystyle \pi } を使って解答するのが一般的です。 半径が6センチメートルの円の面積の求め方は次の通りです。 A = π r 2 {\displaystyle A=\pi r^ {2}} A = π 6 2 {\displaystyle A=\pi 6^ {2}} A = 36 π {\displaystyle A=36\pi } または、 A = 36 ( 314) = {\displaystyle A=36 (314)=} 半径aの円の方程式はxy軸で表現すると x²y²=a² よって、 y=±√ (a²x²) です。 面積は∫ydxだから、 a ∫√a²x²)dx a の2倍です。 この ∫√ (a²x²)dx の計算の仕方が、 置換積分 x=acosθ もしくは、x=asinθとするわけです。
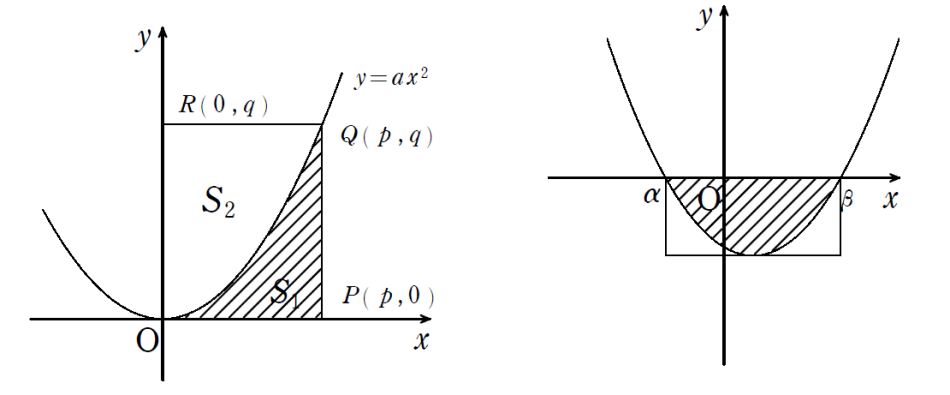



図形を利用した定積分の計算 授業実践記録 数学 高等学校 知が啓く 教科書の啓林館



48s96ub7b0z5f Net Houbutsusen En Menseki




球の表面積と円の面積 球の表面積や円の面積を積分により求める場合 パラメ Okwave




ループの面積 Geogebra




アルゴリズム 2つの円の重なった面積 Teratail




高校数学 定積分と面積 2 問題編 映像授業のtry It トライイット




円の面積の求め方と覚えるコツ なぜ半径 半径 3 14になるか アタリマエ




高校数学 円の中心と弦が作る三角形の面積の最大 受験の月



円の一部の面積と 円の直径があり これらの情報から Xの距離を求 Yahoo 知恵袋



球の表面積の公式の求め方




数値積分による円の面積の計算 Java プログラミング 入門



Q Tbn And9gcs8govrxmmsri Uq2ku4tuxauhmioafyuowrywnpq8yleyditf9 Usqp Cau




高校数学 定積分と面積 2 問題編 映像授業のtry It トライイット



重積分の計算



球の表面積 立体の表面積が影の面積の4倍になること 数学と社会の架け橋 数学月間




数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ




円 扇形 の面積 周や弧の長さの公式 数学fun
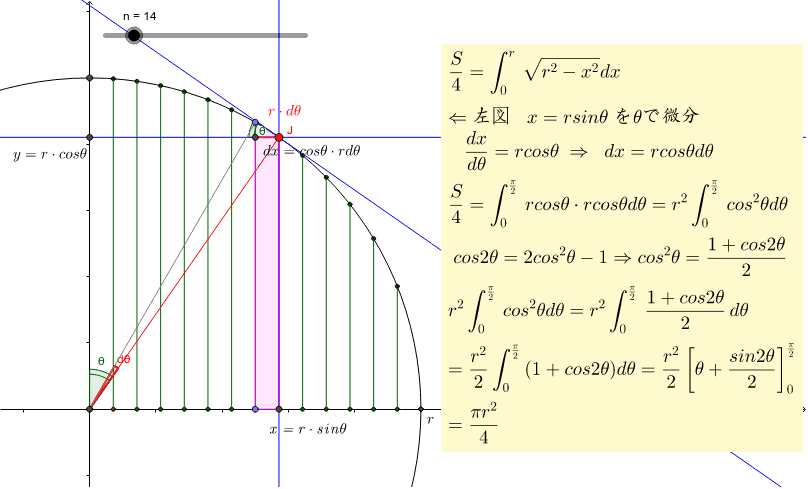



円の面積 置換法の意味 Geogebra



面積分



球帯と球冠
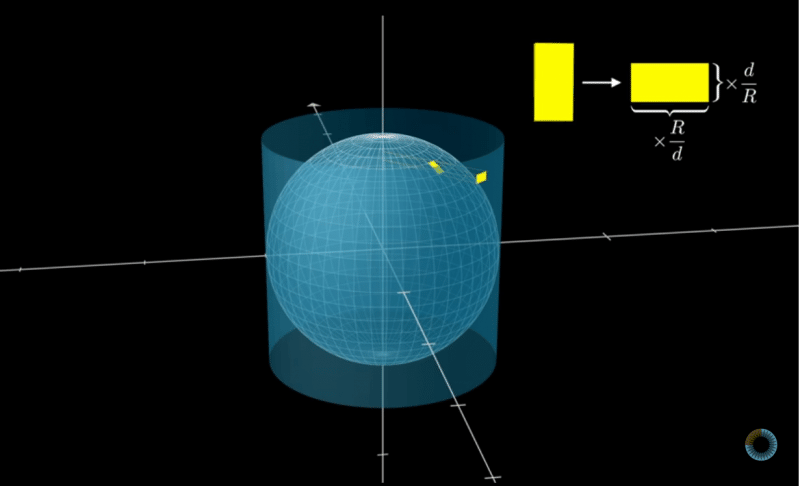



球の表面積 Sgk Note




円周 Wikipedia




球の体積公式の微分が表面積になっている理由 Youtube



円の面積の公式 この問題をやれば円の面積は余裕だぜ 三重の個人契約家庭教師



気まぐれ Net 図を用いた円の面積の求め方 公式を使わずに



いわき市 全校表示 へ いわき小中学校ホームページ



3 円の面積 数値積分の台形公式




電気磁気工学を学ぶ 積分と円の面積



高校数学 放物線と円の間の面積 受験の月




領域 連立不等式の範囲を図示する方法と格子点と面積の求め方



円と帯の共通部分の面積 Den Of Hardworking



1




数学を楽しむ 面積分




数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ



数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ



ほのぼの数学頑張ろう



面積を求める
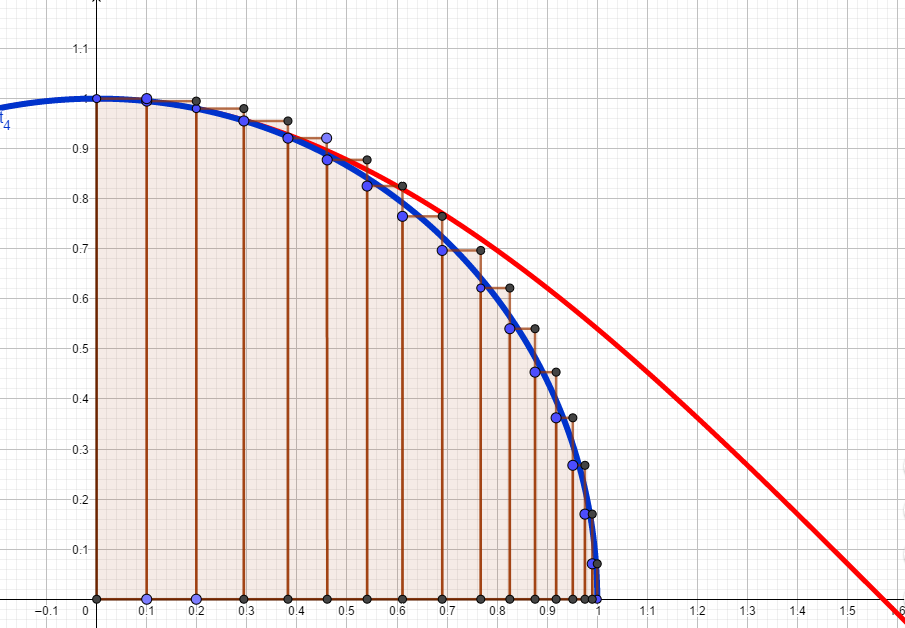



置換積分のイメージ 極小をさらに縮める キソカラ




円の面積の公式 算数の公式
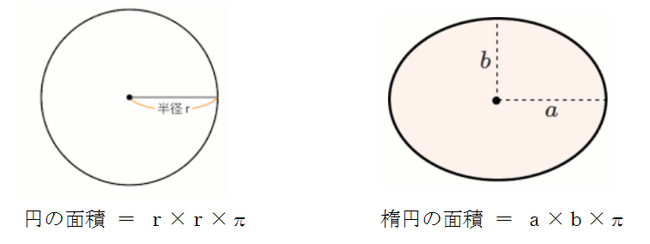



楕円の面積の公式 小学生でもわかる計算問題を紹介するぞ 三重の個人契約家庭教師




Python演算処理 半径 直径 円周長 円の面積 球の表面積 球の体積の計算上の往復 Qiita




高校数学 定積分と面積 2 問題編 映像授業のtry It トライイット
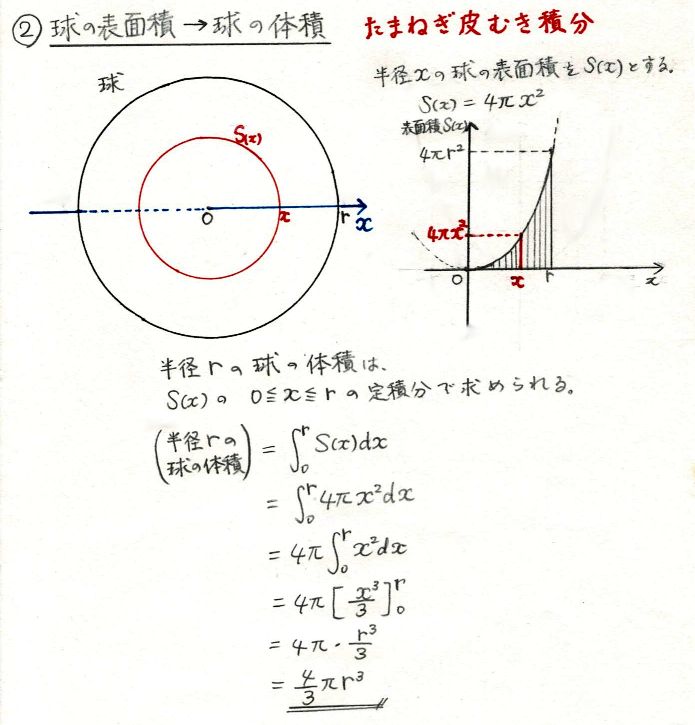



数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ




6年算数 円の面積 なぜ 半径 半径 円周率になるのか 解説します Youtube



円と放物線に囲まれた面積 微分法と積分法 おおぞらラボ




円の部分面積と部分円周を教えてください 添付にある円のcの面積と 数学 教えて Goo



なぜ円の面積 P 半径 半径 なのでしょうか 簡単に証明方法はあるのでしょうか Quora




積分法の話題3 放物線と円とで囲まれた部分の面積 高校数学 身勝手な主張




高校生向け 積分 円の面積 Youtube



面積を求める




ジョゼフ アンリ 見掛け倒しの問題ですね 定積分の表す部分の面積が円の面積の1 4でしかないですね
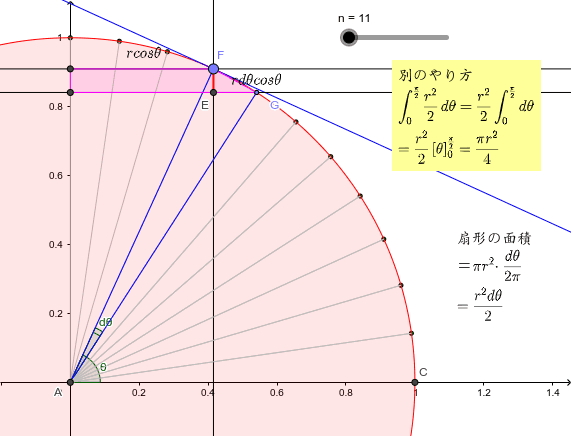



円の面積2 Geogebra




極方程式の面積 扇形積分 おいしい数学




みかんとバームクーヘン エセ化学者の理科の学校




赤波線の部分なのですが 半径2の半円の面積を表すとありますが どのように判断すれば良 Clear



数学 積分を使って面積や体積を計算する方法を分かりやすく解説
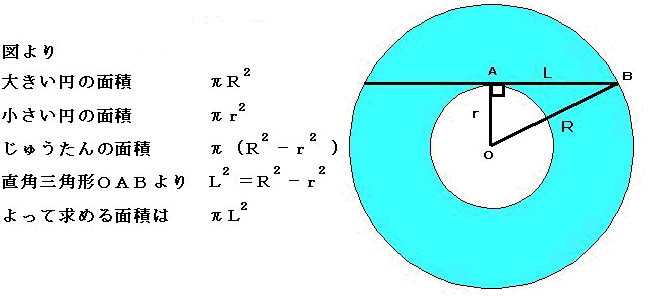



Mondai21



円の面積を積分で計算する2通りの方法 具体例で学ぶ数学



円の面積の公式 算数の公式



面積分



Sphere 01




円の面積の公式 円周の求め方と間違えないようにしよう 中学や高校の数学の計算問題
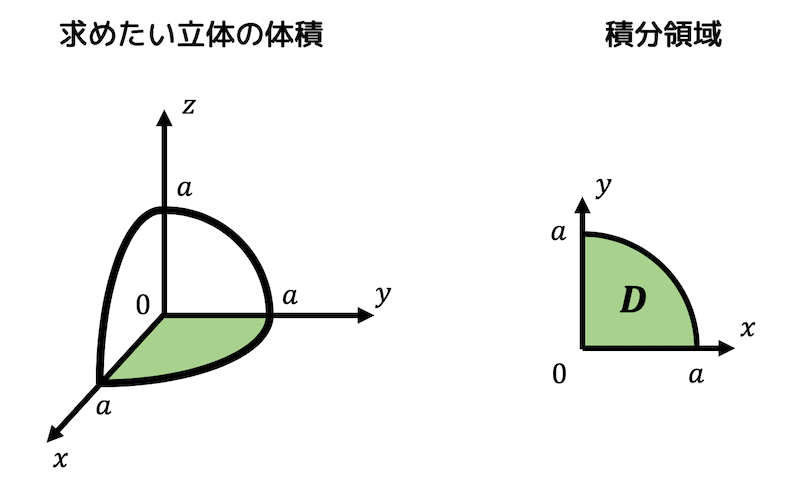



うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾



3



積分計算による体積の求め方 断面積の積分や回転体の体積 受験辞典



この積分が半円の面積を示しているのは何故でしょうか Yahoo 知恵袋




高校数学 楕円の面積と回転体の体積 受験の月




球の表面積と体積の公式 数学fun




円の面積の求め方 公式と計算例
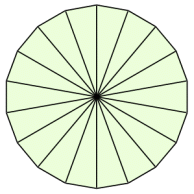



積分 円の面積の再考 大人が学び直す数学




球の体積 球の表面積の公式の導出 積分 優技録
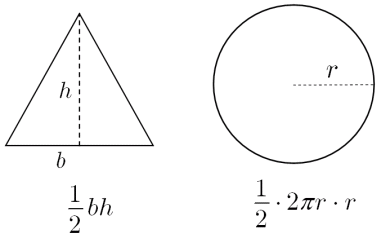



積分 円の面積の再考 大人が学び直す数学



1




標準 楕円で囲まれた部分の面積と積分 なかけんの数学ノート




楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ




うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾




三角形の面積を外接円の半径を使って求める Schoolmath S Diary
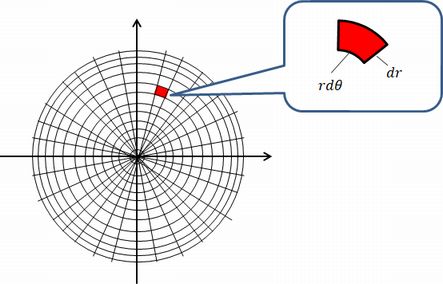



極座標で円の面積を求める方法の補足 おにノート おーにしの物理 数学ノート




円の面積の求め方を考えよう 小学校6年生の算数教材から 身勝手な主張




円の面積 練習応用 Youtube




勉強しよう数学 円の面積を積分で求める




弓形の面積 香料ゐっすゐの夢
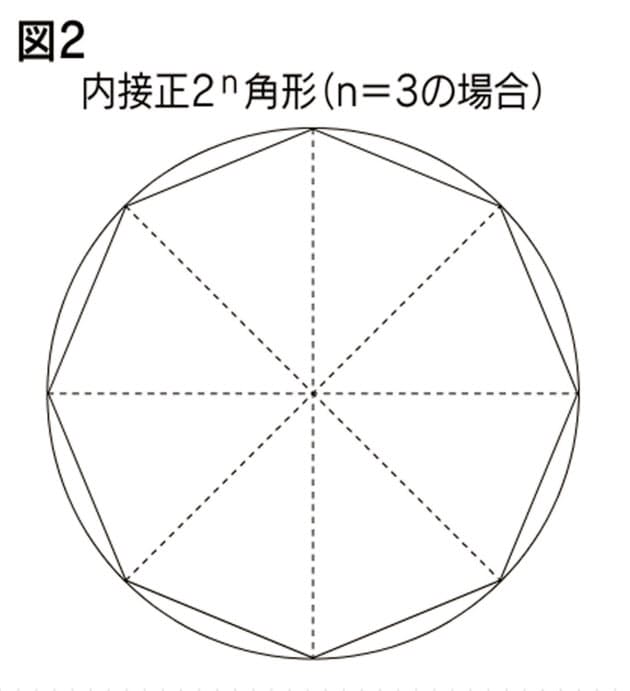



子供に説明できる 円の面積の公式 の証明 Nikkei Style
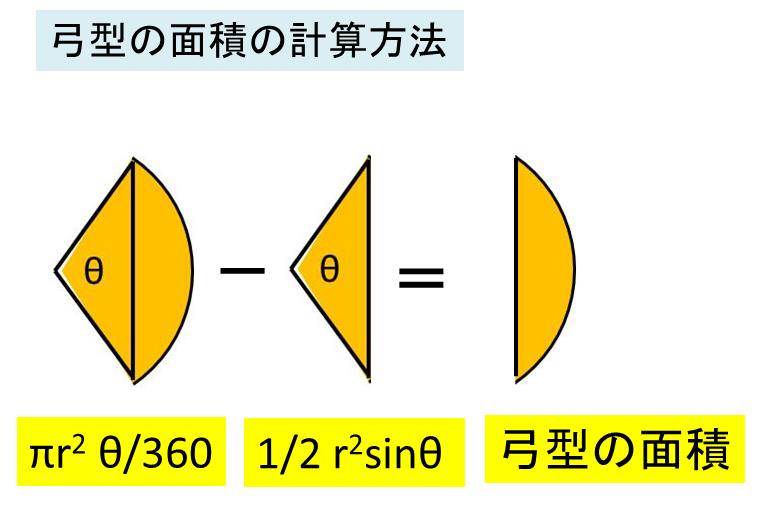



欠けた円 欠円 や弓形の面積の計算方法




𓊆 数 定積分 𓊇 1枚目と2枚目は どちらも X の Clear
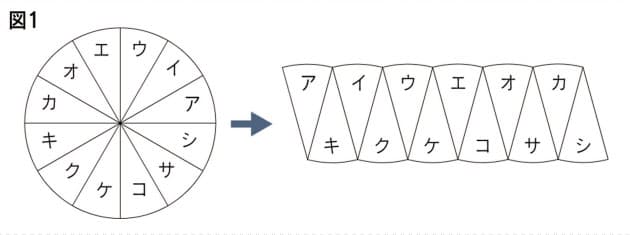



子供に説明できる 円の面積の公式 の証明 Nikkei Style




勉強しよう数学 球の表面積を積分で求める



年5月26日 積分の妙 チェリー個人指導学習塾 佐倉市



0 件のコメント:
コメントを投稿